Legyen Mat-S az a kategória, melynek objektumai a nemnegatív egészek és az n->k morfizmusai az nxk dimenziós mátrixok az S félgyűrű felett. Pl. ha S a nemnegatív egészek félgyűrűje, akkor az n->k morfizmusok éppen azon nxk dimenziós mátrixok, melyeknek minden rublikájában nemnegatív egész szerepel.
A morfizmuskompozíció a mátrixszorzás.
Vegyük észre, hogy minden n >= 0 -ra létezik pontosan egy 0->n morfizmus, ez pedig az üres leképezés. Hasonlóan, az egyetlen n->0 morfizmus az üres leképzés.
Fel fogjuk szerelni Mat-S kategóriát némi extra struktúrával.
Legyen A egy nxk és B egy mxp mátrix. Ekkor legyen
a következő (n+m)x(k+p) dimenziós mátrix:
A fenti sor egy kétváltozós funktort definiál
Mit lehet megállapítani erről a kétváltozós funktorról? Asszociatív és egységelemes. Az egységelem az egyetlen 0->0 morfizmus.
A következő példa arra világít rá, hogy a speciális esetek miként vannak lekezelve. Jelölje F az egyetlen n->0 morfizmust és A egy tetszőleges k->p morfizmust. Ekkor
egy (n+k)xp dimenziós mátrix.
Most nézzük Set kategóriát. Set is ellátható extra struktúrával a következő módon. Legyenek f és g relációk. Ekkor
-t az f és g direkt összegének, azaz f + g -nek definiáljuk. Az indukált
funktorra is igaz, hogy egységelemes. Az egységelem az üres reláció az üres halmaz felett. De... asszociatív?
Nem az! Ugyanis A és B halmazok direkt összege a következő halmaz
és behelyettesítve látjuk, hogy vannak olyan A, B, C halmazok, hogy (A+B)+C nem egyenlő A+(B+C)-vel.
Nem egyenlő, de izomorf ! Azaz, léteznek Set-beli morfizmusok
és
melyekre igaz, hogy
Ekkor azt mondjuk, hogy
izomorfizmusok.
Hmmm. Mintha valamiféle kapcsolat lenne Set és Mat-S között, nem igaz? Mintha ugyanazon fogalomnak lennének különböző, konkrét példányai. Ez a megfigyelés vezet a következő definícióhoz:
Szimmetrikus monoidális kategória alatt egy rendezett hetest értünk, ami a következőekből áll:
egy kategória: C
egy kétváltozós funktor, a monoidális funktor:
egy objektum C-ben, a monoidális funktor egységeleme: 1
egy C-beli izomorfizmus:
egy C-beli izomorfizmus:
egy C-beli izomorfizmus:
egy C-beli izomorfizmus:
Megköveteljük, hogy ezek a morfizmusok eleget tegyenek bizonyos feltételeknek. Ezen feltételek szükségesek és elegendőek ahhoz, hogy igaz legyen, hogy tetszőleges X és Y objektumokra legfeljebb egy darab olyan X->Y morfizmus létezik, mely kifejezhető az
morfizmusokból ill. inverzeikből kompozíció és a monoidális funktor segítségével.
Egy ilyen feltételt fejez ki a következő pentagon:
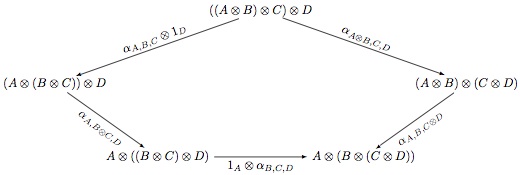
Egy pillanatra felejtsük el a kategóriákat és vegyük az
szót. Ezt a szót az
átírási szabály segítségével kétféleképpen tudjuk átzárójelezni úgy, hogy eredményül a
szót kapjuk. A pentagon fölső sarkából a jobb alsó sarokba vezető két út éppen ezt a két átzárójelezést reprezentálja. A pentagon azt fejezi ki, hogy ezt a két különböző átzárójelezést azonosítjuk. Ennek következménye, hogy ha megköveteljük azt, hogy a pentagon kommutáljon (azaz azt, hogy a fölső sarokból a jobb alsó sarokba vezető utak címkéit sorrendben összekompozíciózva mindkét esetben ugyanazt a morfizmust kapjuk) akkor bármely X, Y objektumokra igaz, hogy legfeljebb egy darab X->Y (izo)morfizmus van, mely az
morfizmusokból fejezhető ki, kompozícióval és a monoidális funktorral.
Egy másik hasonló feltételt fejez ki a következő háromszög:
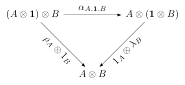
További feltételeket teszünk még a következő morfizmusokra:
és 1-re vonatkozólag, de ebbe nem kívánok jobban belemerülni egy blogposzt formájában. A lényeg az amit már leírtam: a szimmetrikus monoidális kategória definíciójából adódik, hogy tetszőleges X és Y objektumokra legfeljebb egy darab olyan X->Y izomorfizmus létezik, mely kifejezhető az
morfizmusokból ill. inverzeikből kompozíció és a monoidális funktor segítségével.
Példák szimmetrikus monoidális kategóriákra:
Set és Rel, a direkt szorzattal, direkt összeggel
Mat-S, Reg-Δ a direkt összeggel
Vec-k a tenzor szorzattal




