Kategória alatt egy rendezett négyest értünk, mely a következőkből áll.
Vannak objektumaink:
morfizmusaink:
ahol minden morfizmushoz jár egy-egy objektum pár, az adott morfizmus rangja, továbbá adott egy kompozíció művelet az illeszkedő morfizmusokon:
Minden objektumhoz jár egy kitüntetett morfizmus, az adott objektum feletti identitásmorfizmus:
továbbá megköveteljük, hogy a kompozíció legyen asszociatív:
és egységelemes:
Ennyi. Milyen példák vannak kategóriára? Rengeteg....
Először is nézzünk egy konkrét példát!
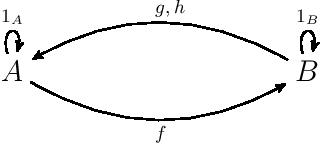
Az ábrán látható kategóriának két objektuma van: A és B, valamint öt morfizmusa: f, g, h és az identitásmorfizmusok. A morfizmuskompozíciót definiáljuk úgy, hogy
és
Rel az a kategória, melynek objektumai a halmazok, a morfizmusok A-ból B-be pedig a relációk AxB felett. Morfizmusok kompozíciója relációkompozícióval adott, az identitásmorfizmus pedig az egyenlőség reláció AxA felett.
Set az a kategória, melynek objektumai a halmazok, a morfizmusok A-ból B-be pedig az A->B leképezések. Morfizmuskompozíció a szokásos függvénykompozíció, az identitásmorfizmus továbbra is az AxA feletti egyenlőség reláció.
Vec-k az a kategória, melynek objektumai a véges dimenziós vektorterek a k test felett, a morfizmusok pedig a lineáris leképezések. Az identitásmorfizmus a helyben hagyó leképezés.
Z az a kategória, melynek objektumai az egész számok, és A-ból B-be akkor és csak akkor létezik morfizmus, ha A kisebb vagy egyenlő B-vel.
Reg-Δ az a kategória, melynek objektumai a természetes számok, a morfizmusok A-ból B-be pedig az AxB dimenziós mátrixok a Δ ábécé feletti reguláris nyelvek félgyűrűje felett. A morfizmuskompozíció ez esetben a mátrixszorzás.
