Kategóriaelmélet

A blog elköltözött, mert ronda volt. Az új és sokkal esztétikusabb blogom a következő címen található:

http://hajgato.blogspot.hu/

Legyen Mat-S az a kategória, melynek objektumai a nemnegatív egészek és az n->k morfizmusai az nxk dimenziós mátrixok az S félgyűrű felett. Pl. ha S a nemnegatív egészek félgyűrűje, akkor az n->k morfizmusok éppen azon nxk dimenziós mátrixok, melyeknek minden rublikájában nemnegatív egész szerepel.
A morfizmuskompozíció a mátrixszorzás.

Vegyük észre, hogy minden n >= 0 -ra létezik pontosan egy 0->n morfizmus, ez pedig az üres leképezés. Hasonlóan, az egyetlen n->0 morfizmus az üres leképzés.

Fel fogjuk szerelni Mat-S kategóriát némi extra struktúrával.
Legyen A egy nxk és B egy mxp mátrix. Ekkor legyen

a következő (n+m)x(k+p) dimenziós mátrix:

A fenti sor egy kétváltozós funktort definiál

Mit lehet megállapítani erről a kétváltozós funktorról? Asszociatív és egységelemes. Az egységelem az egyetlen 0->0 morfizmus.

A következő példa arra világít rá, hogy a speciális esetek miként vannak lekezelve. Jelölje F az egyetlen n->0 morfizmust és A egy tetszőleges k->p morfizmust. Ekkor

egy (n+k)xp dimenziós mátrix.
Most nézzük Set kategóriát. Set is ellátható extra struktúrával a következő módon. Legyenek f  és g relációk. Ekkor

-t az f és g direkt összegének, azaz f + g -nek definiáljuk. Az indukált

funktorra is igaz, hogy egységelemes. Az egységelem az üres reláció az üres halmaz felett. De... asszociatív? 
Nem az! Ugyanis A és B halmazok direkt összege a következő halmaz 

és behelyettesítve látjuk, hogy vannak olyan A, B, C halmazok, hogy (A+B)+C nem egyenlő A+(B+C)-vel. 
Nem egyenlő, de izomorf ! Azaz, léteznek Set-beli morfizmusok

és

melyekre igaz, hogy 

Ekkor azt mondjuk, hogy

izomorfizmusok.

Hmmm. Mintha valamiféle kapcsolat lenne Set és Mat-S között, nem igaz? Mintha ugyanazon fogalomnak lennének különböző, konkrét példányai. Ez a megfigyelés vezet a következő definícióhoz:  

Szimmetrikus monoidális kategória alatt egy rendezett hetest értünk, ami a következőekből áll:

egy kategória: C

egy kétváltozós funktor, a monoidális funktor: 

egy objektum C-ben, a monoidális funktor egységeleme: 1

egy C-beli izomorfizmus:

egy C-beli izomorfizmus:

egy C-beli izomorfizmus:

egy C-beli izomorfizmus:

Megköveteljük, hogy ezek a morfizmusok eleget tegyenek bizonyos feltételeknek. Ezen feltételek szükségesek és elegendőek ahhoz, hogy igaz legyen, hogy tetszőleges X és Y objektumokra legfeljebb egy darab olyan X->Y morfizmus létezik, mely kifejezhető az 

morfizmusokból ill. inverzeikből kompozíció és a monoidális funktor segítségével. 

Egy ilyen feltételt fejez ki a következő pentagon:

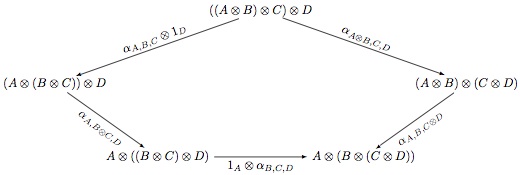
Egy pillanatra felejtsük el a kategóriákat és vegyük az

szót. Ezt a szót az

átírási szabály segítségével kétféleképpen tudjuk átzárójelezni úgy, hogy eredményül a

szót kapjuk. A pentagon fölső sarkából a jobb alsó sarokba vezető két út éppen ezt a két átzárójelezést reprezentálja. A pentagon azt fejezi ki, hogy ezt a két különböző átzárójelezést azonosítjuk. Ennek következménye, hogy ha megköveteljük azt, hogy a pentagon kommutáljon (azaz azt, hogy a fölső sarokból a jobb alsó sarokba vezető utak címkéit sorrendben összekompozíciózva mindkét esetben ugyanazt a morfizmust kapjuk) akkor bármely X, Y objektumokra igaz, hogy legfeljebb egy darab X->Y (izo)morfizmus van, mely az

morfizmusokból fejezhető ki, kompozícióval és a monoidális funktorral. 

Egy másik hasonló feltételt fejez ki a következő háromszög:

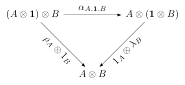
További feltételeket teszünk még a következő morfizmusokra:

és 1-re vonatkozólag, de ebbe nem kívánok jobban belemerülni egy blogposzt formájában. A lényeg az amit már leírtam: a szimmetrikus monoidális kategória definíciójából adódik, hogy tetszőleges X és Y objektumokra legfeljebb egy darab olyan X->Y izomorfizmus létezik, mely kifejezhető az 

morfizmusokból ill. inverzeikből kompozíció és a monoidális funktor segítségével.

Példák szimmetrikus monoidális kategóriákra:

Set és Rel, a direkt szorzattal, direkt összeggel
Mat-S, Reg-Δ a direkt összeggel
Vec-k a tenzor szorzattal

A továbbiakban szükségünk lesz arra, hogy össze tudjuk hasonlítani az egyes kategóriákat.
Ha felírkálunk pár természetesen előforduló kategóriát azt tapasztalhatjuk, hogy sok esetben előfordul, hogy egy C kategóriából megkapható valami D kategória úgy, hogy bizonyos (esetleg végtelen sok) C-beli objektumot és morfizmust azonosítunk. Egy olyan fogalom kell, amely segítségével ki lehet fejezni ezt a kapcsolatot C és D között.

Legyenek C és D kategóriák. Egy

funktor alatt egy leképezést értünk, mely C morfizmusait D morfizmusaiba képezi. További feltétel még, hogy F a C-beli identitásmorfizmusokat D-beli identitásmorfizmusba vigyen, valamint, hogy kompatibilis legyen a morfizmuskompozícióval. Azaz, precízen leírva a következőeket követeljük meg:

minden A C-beli objektumra:

és

minden

C-beli morfizmusokra:

Itt azt a D-beli objektumot jelöli, amelyre igaz, hogy F az A feletti identitásmorfizmust az F(A) objektum feletti identitásmorfizmusba viszi.

Például a következő sorban definiált leképezés egy funktor
Részletesebben, legyen egy morfizmus Set-ben, azaz egy leképezcsés az A, B halmazok között. Mivel minden leképezés reláció is f egy morfizmus Rel-ben. Következésképpen F megőrzi az identitásmorfizmusokat és kompatibilis a morfizmuskompozícióval. Tehát F egy funktor.

Egy újabb példa. Vegyük azt az leképezést, melyre igaz, hogy minden identitásmorfizmust helyben hagy. Tehát ha n egy nemnegatív egész, akkor Továbbá, ha morfizmus Reg-Δ-ban, akkor F(f) legyen az egyetlen n->k morfizmus Z-ben. Kész. Ez is egy funktor! ..... vagy mégsem ?  

Ugyanis Z-ben csak akkor van morfizmus n->k -ba, ha n =< k. És nyilván létezik nxk dimenziós mátrix még akkor is, ha n =< k. Tehát van olyan morfizmus Reg-Δ-ban, amelynek nincs képe Z-ben. Hiszen korábban azt írtam: ha f: n-> k morfizmus Reg-Δ-ban, akkor F(f) legyen az egyetlen n->k morfizmus.

Itt is megmutatkozik, hogy nem minden mondatnak van értelme. A kutatás egyik kulcsfontosságú lépése az, hogy minden pillanatban megkérdőjelezzem azt amit éppen leírtam vagy kigondoltam. Mi a jelentése az egyes szavaknak? Biztos, hogy van értelme? Mi van a szélsőséges esetekkel?

Kategória alatt egy rendezett négyest értünk, mely a következőkből áll.

Vannak objektumaink:

morfizmusaink:

ahol minden morfizmushoz jár egy-egy objektum pár, az adott morfizmus rangja, továbbá adott egy kompozíció művelet az illeszkedő morfizmusokon:

Minden objektumhoz jár egy kitüntetett morfizmus, az adott objektum feletti identitásmorfizmus:

továbbá megköveteljük, hogy a kompozíció legyen asszociatív:

és egységelemes:

Ennyi. Milyen példák vannak kategóriára? Rengeteg....

Először is nézzünk egy konkrét példát!

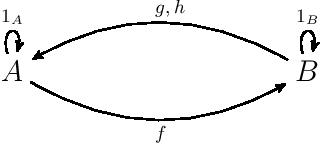
Az ábrán látható kategóriának két objektuma van: A és B, valamint öt morfizmusa: f, g, h és az identitásmorfizmusok. A morfizmuskompozíciót definiáljuk úgy, hogy

és

Rel az a kategória, melynek objektumai a halmazok, a morfizmusok A-ból B-be pedig a relációk AxB felett. Morfizmusok kompozíciója relációkompozícióval adott, az identitásmorfizmus pedig az egyenlőség reláció AxA felett.

Set az a kategória, melynek objektumai a halmazok, a morfizmusok A-ból B-be pedig az A->B leképezések. Morfizmuskompozíció a szokásos függvénykompozíció, az identitásmorfizmus továbbra is az AxA feletti egyenlőség reláció.

Vec-k az a kategória, melynek objektumai a véges dimenziós vektorterek a k test felett, a morfizmusok pedig a lineáris leképezések. Az identitásmorfizmus a helyben hagyó leképezés.

Z az a kategória, melynek objektumai az egész számok, és A-ból B-be akkor és csak akkor létezik morfizmus, ha A kisebb vagy egyenlő B-vel.

Reg-Δ az a kategória, melynek objektumai a természetes számok, a morfizmusok A-ból B-be pedig az AxB dimenziós mátrixok a Δ ábécé feletti reguláris nyelvek félgyűrűje felett. A morfizmuskompozíció ez esetben a mátrixszorzás.

Üdvözlök minden látogatót, Hajgató Tamás vagyok és ez a blog csupa olyat fog tartalmazni, ami engem érdekel. Azaz, elsősorban matematikai jellegű témákat.

A valóság megismerésének egyetlen hiteles módja a tudományos módszer, melynek egyik leglényegesebb eleme a kétely. A hit a kétely ellentéte - vagyis a valóság megismerésére való törekvések tudatos akadályozása.
Aki "hisz" vagy "nem hisz" az már előre eldöntötte, hogy hogyan van a szóban forgó dolog, vagyis valójában nem érdekli, hogy hogyan van. Akit érdekel valami, az kételkedik benne.

A tudományos módszer lényege dióhéjban annyi, hogy a valóságról tett megfigyeléseinkhez modellt építünk, mely magyarázattal szolgál a tapasztaltakra. Egy modell akkor jó, ha minden tapasztalt jelenséget megmagyaráz, prediktív jelleggel bír és helyessége ténylegesen függ minden szóban forgó tényezőtől - tehát nem lehet kivételek sorozata.

Miután megvan a modell, amely a megfigyelt jelenségre hivatott magyarázattal szolgálni, a kétely hajtja az alkotót, hogy elgondolásait közzétegye - annak céljából, hogy bárki aki tud, szabadon beleköthessen, kritizálhassa. És bárki aki bele tud, bele is fog - mindenféle visszatartás nélül, mindenbe, amibe csak bele lehet.

Ha kiderül, hogy valakinek az alapvető elgondolásaiban hiba van, akkor megszégyenülés éri és megtanulja, hogy ne legyen elhamarkodott. Ha egy hiba nem derül ki azonnal, nem kell aggódni - majd kiderül később.

Bár az emberi természet alapján a tekintélyelv is közrejátszhat valamelyest egyes gondolatmenetek helyességének megítélésében - a tudományos világban a kétely a mérvadó. Hiába szavaz mindenki arra, hogy egy állítás igaz, ha az hamis. Ha csak egy ember állítja, hogy a szóban forgó állítás hamis, akkor Neki van igaza és a többiek mind tévednek. Nem az számít, hogy hányan és kik hogyan érzik - hogyan kellene lennie a valóságnak, hanem az számít, hogy hogyan van.

Ahhoz, hogy valaki képes legyen a tudományos módszert alkalmazni a világ megismerésére, elengedhetetlen feltétel az illető személyiségének integritása - meg kell tisztelnie saját magát azzal, hogy soha nem próbálja meg becsapni magát. A kétely és a kíváncsiság hajtja előre - nem tehet úgy, mintha nem venné észre ezt vagy azt a hibát a saját munkájában, nem hazudhatja magának, hogy minden rendben van, ha senki sem fogja észrevenni.

A tudományos világban való boldoguláshoz tehát olyan értékrendszerre van szükség, amely gyökeres ellentétben áll a szociális szférában elvárt "érzékenységgel", ahol a hit erénynek számít és a kétely sértésnek, az önsajnáltatás és önutálat szimpátiát vált ki, míg ha valakinek önbecsülése van és szereti saját magát az csak irigységet, ellenséges reakciókat szül.

Szóval mire jó az, amivel foglalkozom?
A valósághű modellek megalkotásának eszköze matematika.
Ha nem sikerült volna felfedezni a számokat nem lenne lehetőség pénzt használni bármilyen kereskedelem lebonyolításához. A hatos számrendszerben körülményesebb lenne számolni - milyen szerencse, hogy tudunk a tizesről. A sebesség idő szerinti deriváltja a gyorsulás, és komplex számok ismerete nélkül nem állna rendelkezésünkre a kvantummechanika Hilbert-teres formalizmusa. Az én személyes tapasztalatom az, hogy elméleti kutatás (tehát matematika) nélkül az összes matematikára támaszkodó tudományág fejlődése csigamódra belassul egy bizonyos idő után - egész pontosan akkor, amikor az eddig ismert hozzáállásokkal már nem lehet lényegesen javítani az algoritmusokon, amikor a rendelkezésre álló elméleti háttér már nem elég arra, hogy az emberi agy számára kényelmesen és valósághűen modellezzük a tapasztalt jelenségeket.

Viszont nem csak a gyakorlatban lelhetőek fel a matematika alkalmazási területei. A matematikai aktivitást, azaz a bizonyítás folyamatát is lehet modellezni matematikával. Ennek egyik eszköze a logika. És el is érkeztünk oda, hogy milyen céllal indul el ez a blog:

Az ember azt várná, hogy az elsőrendű logikai formulák és bizonyításaik nem alkotnak jó tulajdonságokkal rendelkező algebrai struktúrát, hiszen az összes formuláról és bizonyításról van szó - de ez nem így van. Elsőrendű formulák és bizonyításaik autonóm kategóriát (azaz szimmetrikus monoidális zárt kategóriát) alkotnak.
Sőt! Az is kiderült, hogy kapcsolat van állapotátmeneti rendszerek egyenlőségekkel kifejezhető tulajdonságai és ezen kategóriák egyenlőségekkel kifejezhető tulajdonságai között.
A blogot azzal a céllal indítom, hogy ezt a kapcsolatot járjam körbe a már publikált eredmények alapján.